Pensez à vous abonner sur notre librairie en ligne, c’est grâce à cela que nous tenons bon !
Pas de problème !
Les élèves entrent tranquillement. Onze garçons, six filles. Ils restent debout. S’asseyent. Le problème de la feuille traversée de droites peut commencer.
« Sur une feuille, combien de parties au maximum obtiendra-t-on en traçant 30 droites ? ». Combien de parties… Au maximum… Trente, mais c’est beaucoup ça, trente…
Deux élèves viennent au tableau, présentent leur travail, dessinent des droites, comptent des parties. Leur feuille de conclusion court dans la classe et fait réagir les autres groupes, « Ca ce n’est pas possible, il y a forcément plus de parties là que là. » Alors le reste de la classe va leur poser des questions, dans un débat animé par un maitre de parole. Viviane Monnerville guide, demande des précisions. La classe commente leurs résultats et la discussion s’échauffe : « Mais si, si on a une droite de plus, on a forcément plus de parties ! ». Tiens, c’est vrai, je n’y avais pas pensé. Et on note petit à petit sur le cahier les conclusions trouvées. « Dans le cas de droites parallèles, il y a moins de parties que si elles sont sécantes ou concourantes (elles se croisent en un seul point). »

Suit la même démonstration sur geogebra, par un groupe de garçons. Là, sont vérifiées des compétences portant sur l’utilisation du logiciel. Un autre groupe demande à parler du fameux problème ouvert sur les droites, traité avec un tableau. « Très bonne idée », accepte Viviane Monnerville. « Pour gérer des données, on peut utiliser un tableau. » note-t-on sur un cahier.
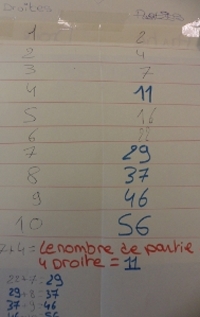
Les filles ont trouvé le résultat jusqu’à 100. Je demande la parole : « Mais… vous voulez dire que vous avez tracé jusqu’à 100 sur des feuilles ? » D’accord, je ne suis pas des plus réactives… Et les filles de m’expliquer patiemment leurs calculs. Et d’insister pour que je prenne les résultats en photo. On rigole pas avec les problèmes ouverts.

Au tour de trois garçons de montrer comment trouver les résultats sur tableur, sans compter. « A3+B4, c’est comme à la bataille navale. » Séance de questions menée par le maitre de la parole. Quand ça déborde un peu le maitre, Viviane Monnerville intervient : « On a un problème ». « Ah oui on parle sans demander ». Et le calme revient. Il y a de la magie dans cette classe…
Il reste cinq minutes. Pas le temps de commencer le travail d’atelier de maths prévu : « Chacun écrit une question dans son cahier une question de maths. » Sofiane lève le doigt : « Qu’est-ce qu’un parallélépipède ? » La sonnerie chante deux fois son laréfa#. La question est notée sur tous les cahiers. Pour le vendredi 24, on répondra à la question de Sofiane…
Les élèves s’envolent, sauf un garçon, Elorn Truong, visiblement peu pressé. J’en profite pour lui demander si quelque chose l’aide particulièrement à apprendre dans cette classe. La réponse fuse : « Ah oui, c’est qu’il y a beaucoup d’exposés ! Et faire des tas recherches aussi. Mes exposés, ceux des autres, c’est cela qui m’aide le plus. A partir de là, on fait la leçon et on comprend mieux parce qu’on a pu poser des questions. » Voilà qui est encore plus clair qu’un problème ouvert…
Christine Vallin








