À deux, devant les élèves

Nous avons cette année mis en place dans chacune de nos classes de seconde un dispositif de co-enseignement. Ainsi, une heure par semaine, deux professeurs de mathématiques sont présents dans la classe[[Administrativement, nous avons demandé à utiliser les heures où la classe est dédoublée. Dans notre dispositif, elle ne l’est plus, c’est un deuxième enseignant qui entre dans la classe. C’est donc un fonctionnement à moyen constants (2 heures profs, 1 heure élève), avec uniquement une contrainte en terme d’emploi du temps des deux enseignants…]] L’objectif principal est d’agir conjointement en classe au plus près des besoins des élèves. Notre analyse croisée des obstacles rencontrés par les élèves dans l’action nous permet ensuite de construire nos parcours d’apprentissage et d’enseignement pour chacune de nos classes et chacun de nous. Notre regard est donc à la fois positionné sur les interactions élèves/professeurs, élèves/élèves, mais aussi professeur/professeur.

Faire vivre une situation en classe

Nous avons proposé aux élèves deux urnes différentes contenant des billes bleues et des billes oranges. Chaque urne contient le même nombre total de billes. Comment faire pour estimer la répartition de chaque couleur dans chaque urne, sans les ouvrir ? Les propositions spontanées des élèves sont notées au tableau.

Sur cet exemple on lit les premières représentations des élèves, prises en note textuellement par un enseignant au tableau : chaque élève peut s’exprimer dans son langage naturel et émettre une opinion. Une élève propose des pesées. Un des enseignants est tenté d’orienter le débat et de ne pas retenir la proposition. L’autre enseignant la note fidèlement au tableau. Ainsi prise en compte par les enseignants et par la classe, l’idée est cependant réfutée par un élève : les billes ont toutes le même poids, il est donc inutile de les peser. Les élèves s’orientent vers un tirage. Ils précisent le « beaucoup de fois » : ils proposent 100, 1000, 33 (effectif de la classe), le triple. Pendant cette phase, les enseignants pilotent conjointement les échanges et interviennent éventuellement pour les relancer.

Sur proposition de la classe, chaque élève tire une bille, on note la couleur, on la remet. On écrit les résultats au tableau. Après observation des premiers résultats, un débat s’engage :

Prof 1 : Que vous inspirent les résultats de ces tirages ?
Elève 1 : Dans le sac il y a plus de billes bleues que de billes orange.
Elève 2 : Dans le sac il y a sûrement… (l’élève hésite)… peut-être… plus de bleues.

La formulation est notée au tableau par l’autre professeur.
Elève 3 : Je ne suis pas tout à fait d’accord, on peut juste dire qu’on a tiré plus de billes bleues.
Prof 1 : Quelle est la différence ?
Elève 3 : Dans le premier cas il s’agit d’une hypothèse alors que dans le second il s’agit d’un fait.
Elève 4 : Il faudrait augmenter le nombre de tirages pour être plus proche de la réalité.
Les élèves se mettent d’accord pour renouveler l’expérience afin d’augmenter le nombre de tirages.

Selon les principes du Débat Scientifique de Marc Legrand[[http://www-irem.ujf-grenoble.fr/spip/spip.php?rubrique61]], « Ces débats il faut apprendre à les introduire avec dynamisme, à les mener avec doigté, à les conclure avec fermeté, à en faire ressortir les éléments clefs dans la partie magistrale ou à les faire revivre à bon escient ailleurs pour rentabiliser “le temps perdu”.  » (Marc Legrand). Intervenir en co-enseignement permet le pilotage des débats et la prise de notes des idées-force nées des échanges en vue d’une trace écrite, mémoire du débat. Dans cette retranscription, on lit la façon dont les élèves font naître spontanément dans un débat collectif la différence entre un fait observé et une hypothèse probabiliste. C’est une des étapes-clé qui mènera à la construction progressive de la notion de probabilité à partir des fréquences observées.

Expérimenter en classe pour construire un parcours d’apprentissage-enseignement

L’activité ci-dessous est donnée aux élèves. L’action se situe dans une grande salle, organisée préalablement pour que les élèves aient de la place pour évoluer librement. Le démarrage de l’activité prend quelques minutes pendant lesquelles les élèves, surpris par la situation, s’agitent. Les enseignants décident de les laisser s’approprier seuls la situation, en se régulant conjointement pour ne pas intervenir. Cette appropriation est une phase importante de l’activité des élèves, ils prennent le temps de s’engager dans l’activité et, très naturellement, ils se répartissent les rôles et se mettent à l’œuvre. Au retour en classe, on recueille leurs observations.

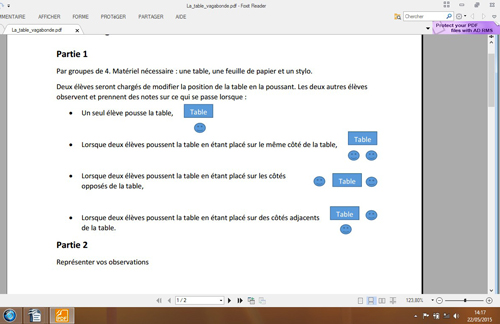
Ci-dessous, les propositions de deux groupes, extraites parmi celles des 9 groupes.

Certains groupes proposent des schématisations de la situation ancrées dans le réel : les tables et les personnes sont représentées, des flèches illustrent les dessins. D’autres choisissent de s’exprimer en mots. L’ensemble de leurs productions, riche de mots et de schémas, constituera la base de la trace écrite de l’activité. Les notions et représentations de mouvement, de déplacement, de force, de vitesse sont extraites. La représentation sous forme de flèche fait consensus. Les notions de direction et de sens sont évoquées à partir de leur langage (« tout droit », « en diagonale », « en arrière »). Les élèves ne se saisissent pas de la différence entre ces deux notions dans un premier temps. En revanche, la représentation de la quantification de la force ou de la vitesse fait débat.

Elève 1 : Quand on pousse à deux ça va deux fois plus vite, on met deux flèches.
Elève 2 : On pousse plus fort !
Professeur : Comment avez vous représenté cela ?
Les élèves montrent et s’expriment autour de la double flèche, présente dans leurs productions.
Professeur : Et pour dix fois ?
Les élèves proposent (photo ci-dessous) :

Les propositions sont notées au tableau par l’un des professeurs pendant que l’autre pilote et régule les échanges.

La représentation de la norme d’un vecteur par la longueur de la flèche n’est pas naturelle et fait obstacle. A l’issue de cette première approche, nous institutionnalisons le terme « vecteur » qui représente par une flèche un déplacement ou une force. Nous choisissons de re-questionner les notions de sens et de direction associées à la notion de norme dans une activité de tri de vecteurs, proposée dans un second palier d’apprentissage. L’enseignement devient collaboratif : la lecture et l’analyse de ce que proposent les élèves nous renseignent sur la nature des obstacles à l’apprentissage. Nous devrons ensuite penser des situations adaptées, prenant en compte ces obstacles, qui constitueront la suite de notre parcours. La construction des savoirs liés à la notion de vecteur ainsi que la notion elle même se fait alors dans le temps, progressivement, dans une action conjointe enseignant – apprenant.

Utiliser les TUICE

Un autre aspect de notre action en classe concerne la prise en main et l’utilisation des outils logiciels et calculatrice. L’établissement dans lequel nous travaillons ne peut pas nous offrir la possibilité d’accéder à des ordinateurs dans une salle de cours traditionnelle. Des enseignants qui souhaitent emmener leurs élèves en salle informatique doivent réserver l’une des salles à l’avance, et prévoir ainsi une séance dite « informatique ». Nous souhaitions que les logiciels informatiques soient utilisés en réponse à un besoin formulé par les élèves dans l’action c’est à dire en tant qu’outil pour faire des mathématiques, à la demande. Nous avons donc sollicité l’accès systématique à la salle informatique lors des séances de co-enseignement, avec une salle de cours contigüe. Les élèves accèdent aux ordinateurs lorsqu’ils en ont besoin avec l’accompagnement d’un des deux adultes, pour l’utilisation d’un tableur, d’un logiciel de cartes mentales, ou d’un logiciel de géométrie dynamique tel que geogebra par exemple. Nous donnons en fin de seconde l’activité suivante :

À la salle de spectacle : Le directeur d’une salle de spectacle sait qu’il reçoit en moyenne 500 spectateurs quand le prix d’une place est de 12,70 €. Il a constaté que chaque réduction de 40 centimes sur le prix d’une place attire 125 spectateurs de plus. Il souhaiterait déterminer le prix d’une place qui lui attirerait la meilleure recette.

A cette époque de l’année, le contrat didactique est construit et accepté par tous : les élèves cherchent d’abord seuls pendant une phase de dévolution d’une vingtaine de minutes, durant laquelle les enseignants n’interviennent pas. Ils écrivent tous leurs premiers essais, même s’ils n’aboutissent pas, quelle qu’en soit la nature (calculs, dessins, schémas,…) dans leur état de connaissance actuel, et formulent leurs besoins. Certains démarrent par des tests sur des exemples numériques. Très vite, ceux-là souhaitent en générer davantage, et réclament l’utilisation d’un tableur (figure 1). D’autres introduisent une variable, calculent la recette à l’aide d’une fonction, et demandent l’accès soit à geogebra pour une lecture graphique de la situation (figure 2), soit à un tableur pour une exploration plus précise de la zone située autour du maximum. A l’issue de la phase de recherche individuelle, les enseignants circulent dans la classe, et accompagnent ceux qui en ont fait la demande dans la salle informatique pour donner suite à leurs recherches.

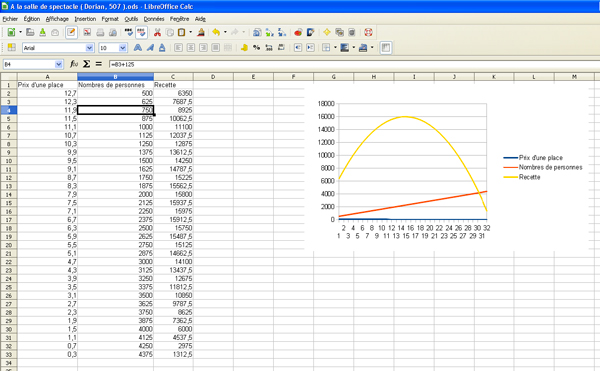
Figure 1

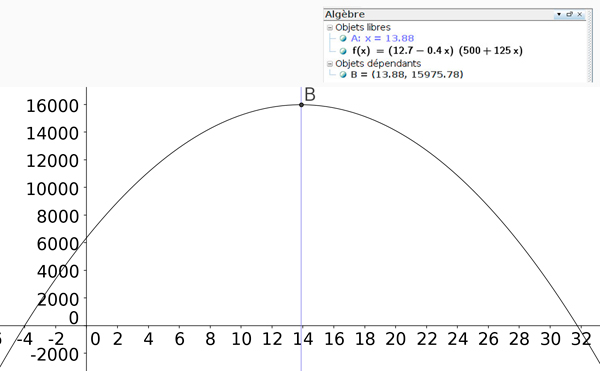
Figure 2

A l’issue de la séance, les productions, qu’elles soient écrites ou numériques, sont recueillies et analysées par les enseignants. Sur la première production, on voit que l’élève fait baisser de 0,40 € en 0,40 € le prix d’une place et obtient une recette maximale de 15 975 € pour une place à 7,10 €. La stratégie ne permet pas une plus grande précision pour le résultat. Le deuxième élève (Figure 2) obtient une valeur plus précise de la recette, 15 975,78 €, en introduisant des outils plus puissants : la variable x représentant le nombre de fois où on applique la réduction, et une fonction qui calcule la recette. Ces deux productions présentées avec d’autres comme objet de débat à la classe, amèneront tous les élèves à franchir une étape de plus dans leur apprentissage. Ils remobilisent leurs savoirs sur les notions de variable et de fonction et en poursuivent les constructions en s’interrogeant sur les particularités sur le second degré. L’utilisation des TUICE facilitée par la présence des deux enseignants a ici un double enjeu : utilisées à la demande des élèves pendant la recherche, elles prennent du sens. De plus, elles participent aussi à construire les savoirs mathématiques puisque la richesse et la diversité des productions auxquelles elles donnent lieu déclenchent chez les élèves de nouveaux questionnements. Ils progressent à leur rythme et acquièrent progressivement les nouveaux savoirs.

Conclusion

Ces trois situations que nous avons vécues en co-enseignement nous ont conduits à envisager notre action enseignante sur un plan coopératif. Les productions des élèves, qu’elles soient orales, écrites ou numériques, recueillies en situation de débat ou de recherche, sont analysées et gérées à deux soit dans l’action de classe, soit dans un temps de concertation. Nous intégrons ensuite les obstacles que nous y lisons dans la suite de nos parcours ou dans le cadre d’une exercisation adaptée. Cela nous permet d’avancer dans nos pratiques et nourrit notre réflexion didactique. Les compétences professionnelles de l’un et de l’autre se complètent et se développent, toujours avec beaucoup de bienveillance et de confraternité. Nous faisons à deux ce que nous n’oserions peut-être pas faire seul, proposant ainsi aux élèves des situations de classe très riches, innovantes, dynamiques, et très bénéfiques pour donner du sens aux mathématiques.

Bertrand Fouques, professeur de mathématiques, lycée Le Verrier
Clarisse Gallien, professeur de mathématiques Lycée Le Verrier et IREM de Caen, groupe didactique école-collège-lycée