Pensez à vous abonner sur notre librairie en ligne, c’est grâce à cela que nous tenons bon !
La ZIP de Shanghaï et les mathématiques
Dans notre groupe de l’IREM de Caen, nous faisons le choix de créer des univers « expérimentables » pour mettre nos élèves dans l’action, de contextualiser, décontextualiser, recontextualiser les apprentissages disciplinaires, pour construire et donner du sens aux savoirs des programmes. Ce qu’énonce Edgar Morin dans le n° 521 des Cahiers pédagogiques « Croiser des disciplines, partager des savoirs[[Cahiers pédagogiques 521, avril 2015, https://www.cahiers-pedagogiques.com/No-521-Croiser-des-disciplines-partager-des-savoirs]] », nous conforte dans notre conception des croisements interdisciplinaires : « la grande lacune de la connaissance disciplinaire, c’est qu’elle découpe arbitrairement les connexions entre les différents objets de connaissance et qu’elle tend à clore l’objet de connaissance hors de son contexte »… La question est bien du comment relier les savoirs sans qu’aucune discipline ne soit lésée, bien au contraire. Mais n’en n’oublions pas de construire les savoirs mathématiques.
Des regards, des échanges une écoute conjointe
Le midi sur le temps du repas ou dans la salle des profs, des conceptions et une motivation partagées et voilà un projet naît entre Marion. B professeur de géographie (la plus jeune du collège) et Claudine. P, professeur de maths (la moins jeune). Nous décidons un atelier en collectif d’enseignement sur La ZIP de Shanghai.
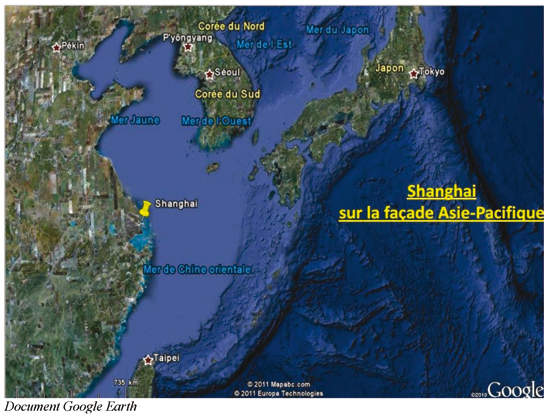
Nous en informons notre principal qui nous demande de lui envoyer notre projet. Il nous fait confiance et contribue au succès de cette expérimentation en nous permettant de disposer de bonnes les conditions : trois séances croisées avec les deux profs en co-intervention précédées ou suivies de deux séances disciplinaires. Aussi nous sommes lancés dans le travail autour d’une situation complexe.
1. Sur le temps disciplinaire
Marion distribue ce document pour situer l’univers d’étude. Puis elle réactive les savoirs et les attributs sur la zone industrialo – portuaire du centre ville de Shangai (Échelle locale)
2. Lors de notre première séance croisée
Marion propose aux élèves de travailler au mieux la représentation schématique de l’espace et les amène à prendre conscience du gigantisme de la ZIP de Shanghai à partir d’ un texte sur la zone industrialo-portuaire de Shanghai.
L’ élève est amené à mobiliser des savoirs mathématiques : distance et échelle, des savoirs géographiques : quel zoom adopter ? Quels figurés associer ? et à faire des calculs et des essais. Il doit se référer à deux registres de langages différents : géographique (document ci- joint) et mathématique.
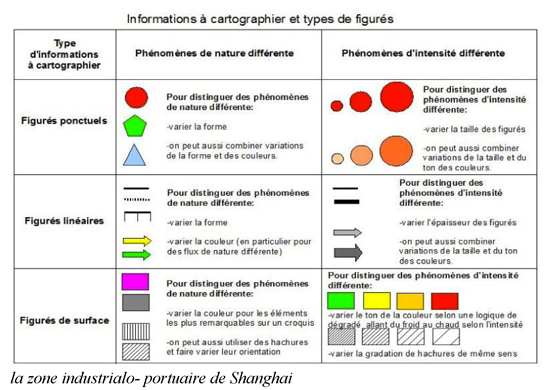
Informations à cartographier et types de figurés
En math : représentation de l’espace ? Point ? Figure ? Échelle ?
En géographie : carte, croquis, schéma, graphique ? Quel Zoom adopter ? Quels figurés associer ?
Deux élèves, Constance et Claire tentent une schématisation de la ZIP et abandonnent devant l’obstacle des trois échelles. Elles veulent souligner dans ce diagramme circulaire le gigantisme de la ZIP en montrant la grande puissance industrielle de Shanghai puisqu’elle assure « plus du tiers de la production nationale de véhicules de tourisme, 50 % de la construction navale et plus de 25 % de la micro-électronique »
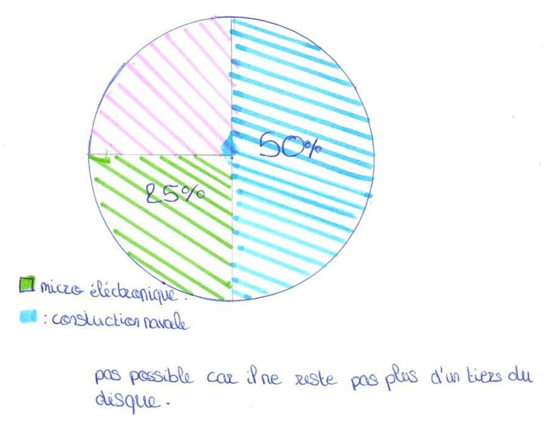
Tentative de schématisation par Constance et Claire
Constance dit : Pas possible, il ne reste pas « plus du tiers ». Un premier argument pour signifier que cette représentation n’est pas adaptée.
Et elles proposent un diagramme en bâtons qu’elles n’ont pas le temps d’achever. Alors que les autres groupes ont opté pour la représentation schématique et ils se sont heurtés au problème de l’échelle.

Diagramme en bâtons
3. Deuxième séance croisée
Comment représenter la production mondiale automobile ? Comment lire toutes ces données du tableau (ci-dessous) ?
Tous partent en salle informatique pour utiliser le tableur et choisir leur graphique.
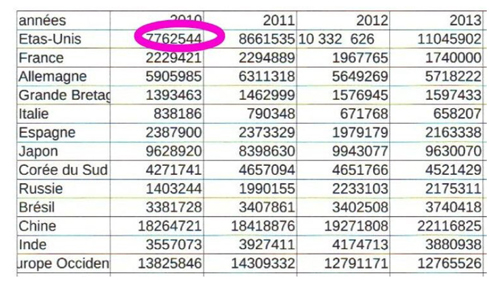
Tableau de la production mondiale automobile
Après quelques essais, les élèves choisissent…
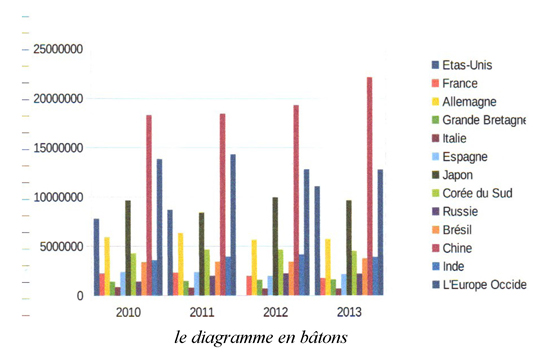
Le diagramme en bâtons (tableur)
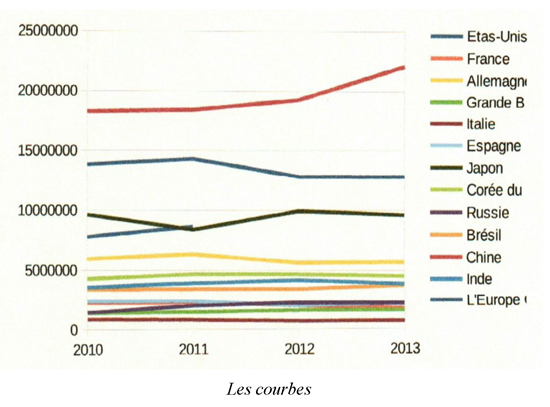
Les courbes
4. De retour en salle de maths
L’enseignante demande à chaque élève de faire sur papier une courbe, constate avec grande satisfaction que tous ont produit, et découvre des représentations différentes commentées, en fonction des obstacles qu’ils ont rencontrés.
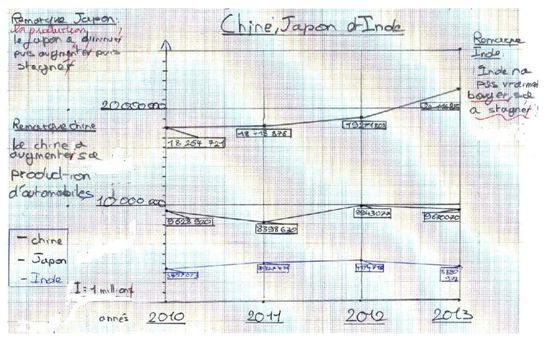
Tableau comparatif Chine, Japon, Inde
Les élèves n’auraient jamais produit ces graphiques commentés s’ils avaient été commandés uniquement dans l’univers mathématique pour eux « décontextualisé » ; le milieu au sens de Guy Brousseau génère une production plus riche.
Ces obstacles récurrents et signifiants de leurs états de connaissance vont devenir l’objet de la construction d’une compétence transversale : faire un graphique. Ces obstacles de toujours sont des objets d’enseignement : Quelle graduation choisir sur les axes ? Quelles grandeurs sur quels axes ?

5. Troisième séance croisée
Les élèves comme les professeurs doivent gérer la polysémie des mots.
Marion me dit : « aujourd’hui je leur donne trois documents pour analyse de texte, il y a des échelles partout ! »
Claudine cherche partout et ose dire : « Je ne comprends pas ce que tu leur as dit, je n’en vois aucune trace ! »
Marion éclate de rire.
Claudine Je n’avais pas cette connaissance sur la polysémie du mot « échelle » dans l’univers géographique.
6. Créer des liens avec les parcours d’apprentissage disciplinaires : décontextualiser
En math, retour sur la séance croisée 2
Les élèves : c’est impossible de représenter précisément ces productions. On a choisi un arrondi.
| Grande Bretagne | 1 393 463 | 1 462 999 | 1 595 084 |
| Grande Bretagne | 1 400 000 | 1 450 000 | 1 600 000 |
| Certains ont écrit : | 1,4 M | 1,45 M | 1,6 M |
Killian : « c’est quand on n’a pas beaucoup de place pour écrire »
Guillaume : « On gagne du temps »
Thomas : « Plus simple à lire »
Vers une nouvelle écriture : l’écriture scientifique d’un nombre
La prof : Et alors comment faire ?
Réponse en collectif :
1,4 M = 1,4 x 1M
= 1,4 x 1 000 000
1,4 M = 1,4 x 106
7. Les élèves ont aimé…
L’utilisation du tableur, choisir leur représentation graphique, mais moins le manque de précision qui leur a permis de comprendre en fait l’essentiel : La fonction d’un graphique qui représente une évolution. Aussi le travail de groupe, le mélange des disciplines « on comprend mieux » et « la découverte de la production automobile mondiale ». Ils ont trouvé du sens à leurs apprentissages.
Et les profs ?
En fait « Innover, n’est ce pas faire à partir de l’ordinaire, de l’extraordinaire ? »
Et alors, quelle suite à cette action ? La fin de l’année scolaire arrive et entre deux portes, on anticipe déjà les projets possibles à venir.
Deux projets pour 2015-2016
Un projet en SVT – Maths sur les marées pour préparer la sortie pédagogique à St Honorine des Pertes avec deux classes de 5e.
Mais aussi un nouveau projet initié par Marion, rattachée à un autre collège. Dès Septembre elle m’envoie un document sur « La cartographie par anamorphose » pour représenter un événement, relais accepté par le collègue qui lui a succédé.
Précédemment les pratiques d’itinéraires de découverte ont participé vivement à nous convaincre de la richesse de ces enseignements croisés et expliquent pourquoi nous aimons innover dans la continuité.
Marion Bellin et Claudine Plourdeau
Collège Albert-Camus, Torigni-sur-Vire, Groupe Didactique de l’IREM- Ifé – PERMES de Caen


